We are exploring the effect of spin population imbalance in a spin-1/2 mixture of fermionic lithium 6. Imbalanced spin populations in a neutral cold atomic gas are analogous to applying a magnetic field to a superconductor, which you might think would cause the spins to point in a preferred direction. Because of the Meissner effect, however, a superconductor will do whatever it can to avoid the penetration of the field into its interior (“I won’t let you in, not by the hair on my chinny, chin, chin!”). Yet, with a large enough applied magnetic field, superconductivity is destroyed in Type I superconductors, while a vortex is created in Type II superconductors. In cold atoms, all we have to do to create an internal “magnetic field” is to unbalance the number of spin-up and spin-down particles – which is easy!
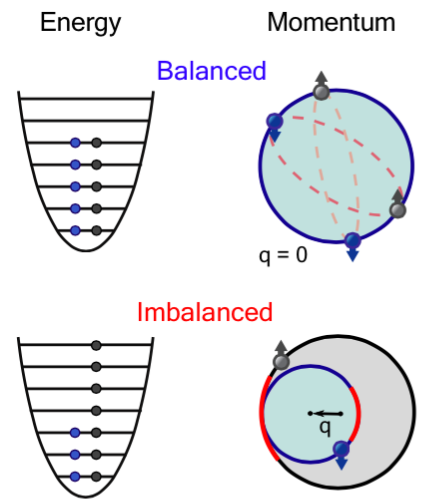
Figure 1: Comparison of balanced BCS pairing and imbalanced FFLO type pairing. In BCS pairing, two opposite spins pair to make their total momentum zero. In FFLO pairing [1,2], the centers of the Fermi momenta shift by an amoount q = kF↑-kF↓, giving non-zero pair momentum.
Our interest is to investigate the possible phases of matter that are created in such a polarized Fermi gas. We are particularly interested in the elusive Fulde-Farrell-Larkin-Ovchinnikov (FFLO) state [1,2]. The FFLO state is an exotic superconductor predicted more than 50 years ago but as of yet, not observed. If found, the FFLO state would be the first to exhibit simultaneous magnetic and superconducting order! It is characterized by an order parameter that is periodically modulated in space, and the spin pairs which make the superconductor have a net center-of-mass momentum, unlike BCS pairs which have zero center-of-mass momentum.
Our first experiments in 2006 demonstrated that a spin imbalanced Fermi gas will undergo a phase separation, as shown in Figure 2 [3]. The central core contains an unpolarized BCS-like superfluid, which is surrounded by a polarized normal shell. Our first experiment was done in a highly elongated trap, for which the domain walls between the phases prevented atoms from freely exchanging from the center to the wings. Thus, the distributions were out of equilibrium and could not be fit to an equilibrium phase diagram.
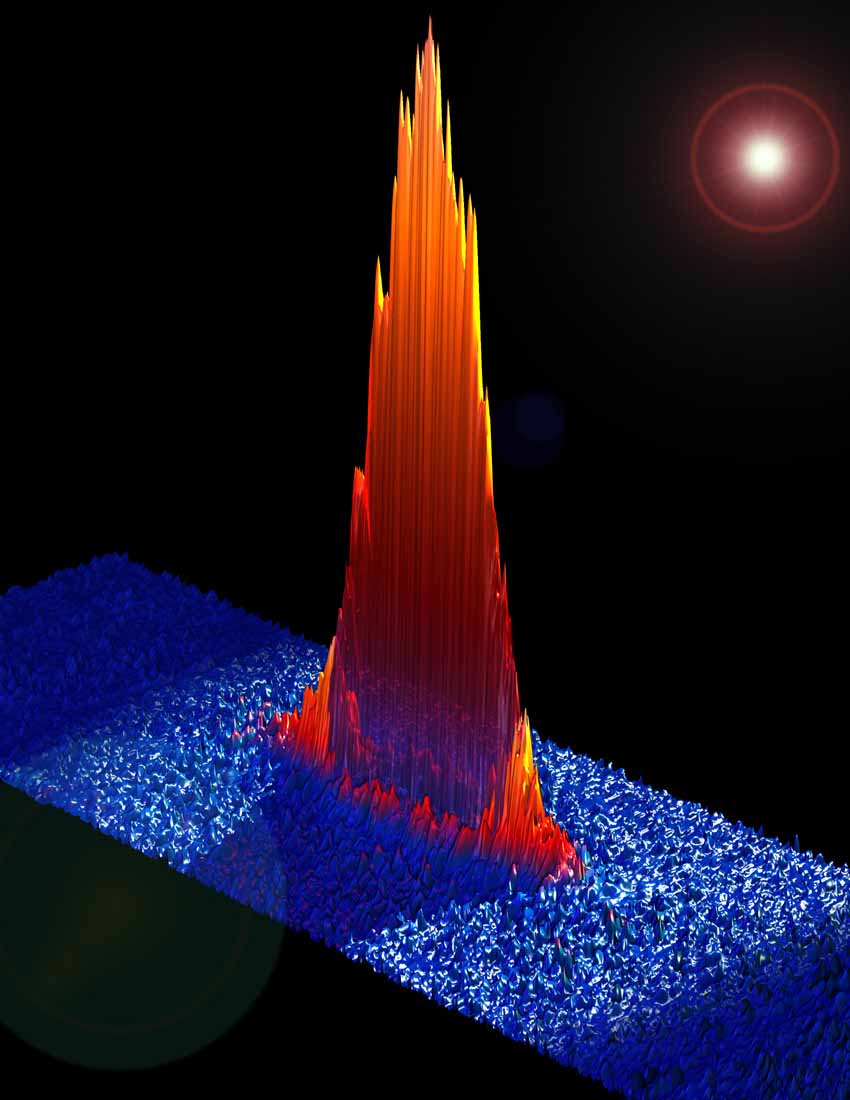
Figure 2: Phase separation seen in lithium.
With our new 3D experiment, the confinement aspect ratio has a more modest value of 3, and we have extracted the equilibrium phase diagram from the density profiles in the trap [4]. We observe four phases: 1) fully polarized non-interacting normal; 2) partially polarized normal; 3) partially polarized superfluid; and 4) unpolarized superfluid. Our phase diagram showing the critical polarization for breaking superfluidity is shown in Fig. 3. The agreement with quantum Monte Carlo (QMC) theory is excellent, and the comparison with previous experiment from MIT is reasonably good. In addition, we determined the equation of state of a balanced Fermi gas in the BEC-BCS crossover regime, as shown in Fig. 4.
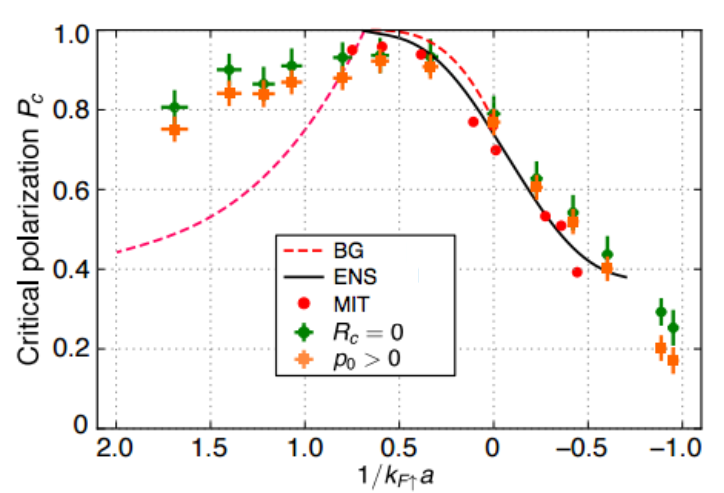
Figure 3: Critical polarization, Pc, as a function of the interaction parameter. The green points indicate the polarization where a balanced superfluid core is no longer supported in the cloud. We find that our data matches both previous data and theory on the BCS side of resonance and the shallow BEC side of the resonance.
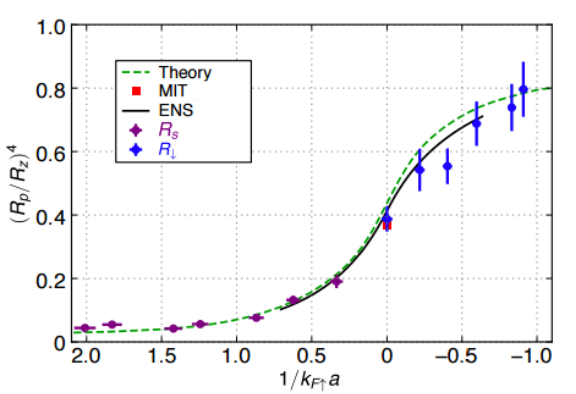
Figure 4: Equation of state as a function of the interaction parameter. We find that our data matches both theory and previous experimental results throughout the BEC-BCS crossover.
But you might be wondering, what about the FFLO phase?? We haven’t seen one! That doesn’t mean that it doesn’t exist, however, and we are still looking. Theory seems to indicate that the FFLO phase might not exist in three dimensions (3D), and if it does, it will be in a very narrow range of parameter space. On the other hand, theory predicts that FFLO completely dominates the phase diagram of a 1D spin-imbalance gas. We have done an experiment using a two-dimensional optical lattice to create a two-dimensional array of 1D tubes to check this prediction. By filling each tube with about 100 spin-imbalanced atoms, we have verified the predicted phase diagram [5] as shown in Fig. 5. In 1D, we see a large, partially polarized central region that theory says is FFLO that is bookended by either completely polarized (normal), or completely unpolarized (superfluid) wings. So phase separation in 1D puts the unpolarized superfluid in the wings while in 3D, it is at the center.
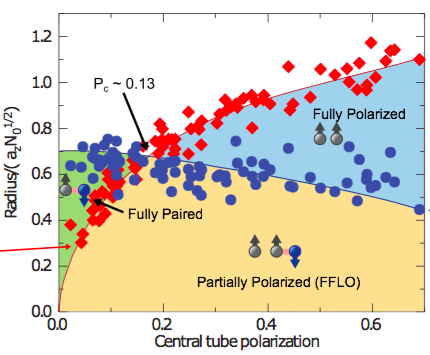
Figure 5: Experimental phase diagram as a function of central tube polarization adapted from Ref. 5. We plot the spin density difference (red diamonds) and the the minority density (blue circles). At the center of the atom cloud, we see a partially polarized phase (yellow region). Depending on polarization, the outer wings of the atomic cloud are either fully paired (green region) or fully polarized (blue region).
Now, we are exploring the cross-over between 3D and 1D. By turning down the strength of the optical lattice, the tubes begin to couple. At weak enough lattice, we see the unpolarized superfluid transition from the wings to the center, as you expect going from 1D to 3D. We are excited about the prospects of observing domain walls, or pairs with non-zero momentum, that would constitute the smoking gun of FFLO physics.
Reference
[1] “Superconductivity in a Strong Spin-Exchange Field”, Peter Fulde, Richard A. Ferrell, Phys. Rev. 135, A550. (1964)
[2] A.I. Larkin, Yu.N. Ovchinnikov, Zh. Eksp. Teor. Fiz. 47, 1136. (1964)
[3] “Pairing and Phase Separation in a Polarized Fermi Gas”, G. B. Partridge, W. Li, R. I. Kamar, Y. Liao, and R. G. Hulet, Science 311, 503 (2006).
[4] “Phase Diagram of a Strongly-Interacting Spin-Imbalanced Fermi Gas”, Ben A. Olsen, Melissa C. Revelle, Jacob A. Fry, Daniel E. Sheehy, and Randall G. Hulet, to be submitted to Physical Review A, arXiv:1508.06362 (2015).
[5] “Spin-imbalance in a one-dimensional Fermi gas”, Y. A. Liao, A. S. C. Rittner, T. Paprotta, W. Li, G. B. Partridge, R. G. Hulet, S. K. Baur, E. J. Mueller, Nature 467, 567 (2010).

