High-temperature superconductivity is one of the great unsolved problems in physics. These materials are paradigms of a class of materials known as strongly correlated fermions, where the mean-field Fermi liquid theory utterly fails. Furthermore, no numerical method is capable of calculating the properties of a macroscopic sample of such a material since the basis size of N fermions increases as 2N. Consequently, nearly 30 years after the discovery of the cuprate materials, we don’t have a complete picture of how these materials become superconducting.
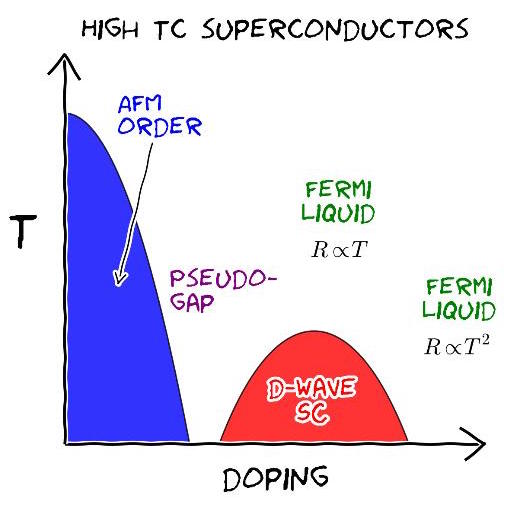
Figure 1: Phase Diagram of High Tc superconductors
While no complete theory of high-temperature superconductivity exists, in 2006 P.W. Anderson suggested that Hubbard model may contain its essential ingredients. The Hubbard model is a highly simplified model for spin-1/2 fermions moving in a periodic lattice. The particles can hop from site-to-site with rate t and they can have on-site interactions U with particles of opposite spin, as shown in the figure below. In the single-band model, however, the Pauli principle forbids two atoms of the same spin on the same site. This simple model exhibits some of the properties of the normal phase of high-Tc materials (see phase diagram below), including an antiferromagnetic Mott insulating phase at half-filling, corresponding to a density of one atom per lattice site. The Néel transition from a Mott insulator with random spins to one with checkboard-like antiferromagnetic order occurs at the exchange energy scale $t^2/U$.
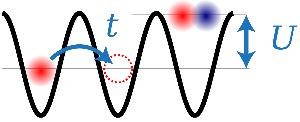
Figure 2: Fermi Hubbard Model
Ultracold atoms in optical lattices are being used to explore many-body physics, such as quantum magnetism in a super-clean and controllable environment. With cold atoms, we can freely tune interactions, density, spin polarization, and even dimensionality enabling the realization of an incredible variety of Hamiltonians. In our lab, we have created an essentially exact realization of the three-dimensional (3D) Hubbard model with an optical lattice and spin-1/2 fermions. The two spin-1/2 states correspond to two hyperfine sublevels of the 6Li atom. The optical lattice is essentially three pairs of orthogonal standing waves created by retroreflecting a 1 um wavelength infrared laser beam.
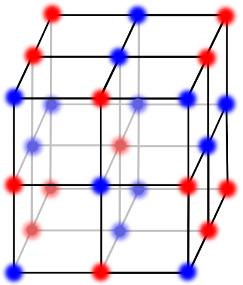
Figure 3: Spin-1/2 Fermions in a 3D Lattice Potential
While most of the relevant parameters of ultracold atoms in optical lattices are within our complete control, achieving sufficiently low temperatures to observe the most interesting phases of matter presents a more formidable obstacle. The transition from a metallic-like phase to an interaction-driven Mott insulator requires that $T < U$, with $U/t \ll 1$. The Hubbard model for spin-1/2 fermions has been realized using ultracold atoms on an optical lattice, and the Mott insulator has been observed by two groups [1,2], but they were unable to cool down to the exchange energy scale of $t^2/U$ to where spins align antiferromagnetically.

Figure 4: Compensated Optical Lattice
We have focused on lowering the temperature in an optical lattice by developing a new method to evaporatively cool in the lattice. We compensate the confining envelope of the IR lattice beams using anti-confining blue-detuned laser beams, as shown in the figures below. By compensating the overall confinement, the chemical potential of the atoms in the lattice can be raised so that atoms evaporate from the edges of the cloud [3]. This scheme has worked and we have cooled deep into the Mott regime [4] and have detected the onset of short-range antiferromagnetic correlations [5].
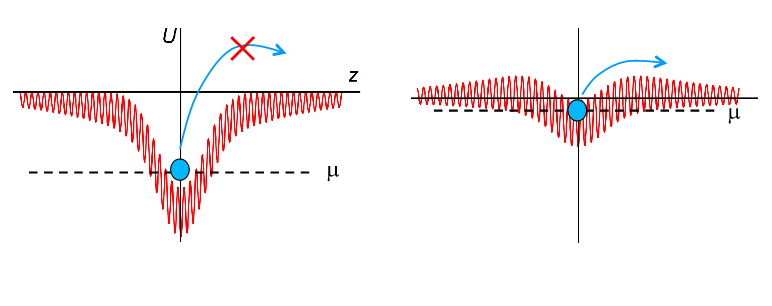
Figure 5: Evaporation with compensating lattice potential
We use spin-sensitive Bragg scattering of light to measure the spin-structure factor, a quantitative measure of the antiferromagnetic correlations in the collection of spins. Spin-sensitive Bragg scattering of near-resonant light is analogous to spin-sensitive neutron scattering in real materials. Measurements of the spin-structure factor are compared to theoretical calculations to establish precise thermometry of the atoms in the lattice, and indicate that T/t = 0.50 (0.04). This is a factor of 2 below the previous lowest temperatures [6].
According to Anderson, if the Hubbard model is doped, so that the density is more or less than one per site, it may also exhibit an interesting high-temperature regime, called the pseudo-gap, and at low enough temperatures, it may form d-wave pairs!
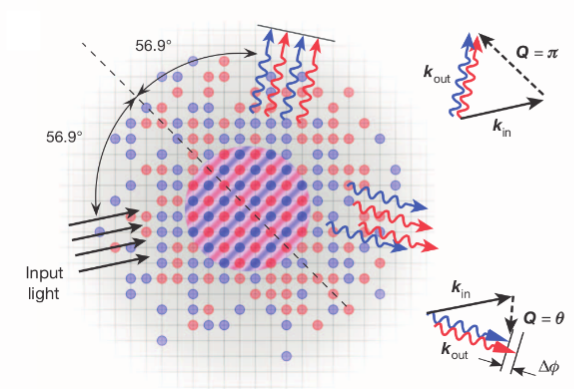
Figure 6: Spin Sensitive Bragg Scattering
Reference
[1] “A Mott insulator of fermionic atoms in an optical lattice”, R. Jördens, N. Strohmaier, K. Günter, H. Moritz, and T. Esslinger, Nature 455, 204-7 (2008).
[2] “Metallic and insulating phases of repulsively interacting fermions in a 3D optical lattice”, U. Schneider, L. Hackermüller, S. Will, T. Best, I. Bloch, T. A. Costi, R. W. Helmes, D. Rasch, and A. Rosch, Science (New York, N.Y.) 322, 1520–5 (2008).
[3] “Enlarging and cooling the Néel state in an optical lattice”, C. J. M. Mathy, D. A. Huse, and R. G. Hulet, Physical Review A 86, 023606 (2012).
[4] “Compressibility of a fermionic Mott insulator of ultracold atoms”, P. M. Duarte, R. A. Hart, T.-L. Yang, X. Liu, T. Paiva, E. Khatami, R. T. Scalettar, N. Trivedi, and R. G. Hulet., Physical Review Letters 114, 070403 (2015).
[5] “Observation of antiferromagnetic correlations in the Hubbard model with ultracold atoms”, R. A. Hart*, P. M. Duarte*, T.-L. Yang, X. Liu, T. Paiva, E. Khatami, R. T. Scalettar, N. Trivedi, D. A. Huse & R. G. Hulet., Nature 519, 211-214(2015).
[6] “Thermodynamics and Magnetic Properties of the Anisotropic 3D Hubbard Model”, J. Imriska et al., PRL 112, 115301 (2014).

