We tune the strength of the interparticle interaction via a collisional resonance known as a Feshbach resonance, where a tunable magnetic field brings a two-body bound state (dimer) into resonance with two interacting free atoms [2]. The plot on the left shows the energies of the weakly bound dimer (blue) and several of the Efimov trimers (red) as a function of the interaction strength a. The trimer states are separated in a by factors of 22.7, and by factors of 22.72=515 in their binding energies. The location of the collisional resonance is where 1/a=0, i.e., the interaction strength becomes infinite. More about how we experimentally determine the scattering length can be found here.
The Efimov trimer state offer additional processes by which atoms can interact. When the trimer binding energy is coincident with the energy of the free atoms (nearly zero energy in the plot) there will be an enhancement in the inelastic collisions that cause loss of atoms from a trapped sample. These locations are called Efimov resonances.
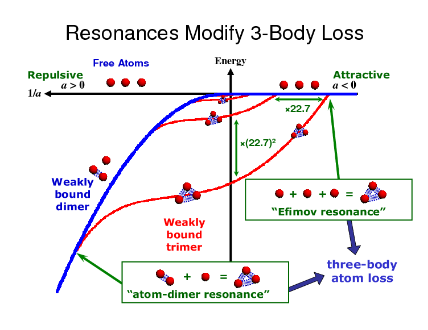
Enhanced loss also occurs when the bound state energy of a trimer is coincident with the energy of a dimer plus a free atom. At this atom-dimer resonance we also expect an increase in the atom loss rate [3].
A quantum interference effect causes a reduction in loss near this atom-dimer resonance.
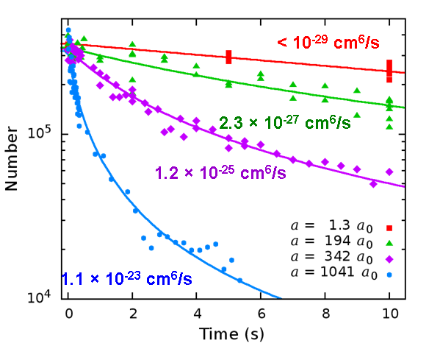
In order to study Efimov physics, we create a trapped ultracold gas of bosonic lithium atoms using methods previously described. When three atoms interact they can recombine into a weakly-bound dimer plus a third atom. This is an inelastic collision, where the binding energy of the dimer is transferred to the kinetic energy of the reaction products, resulting in both the dimer and the third atom being ejected from of the trap. The rate at which atoms leave the trap is dependent on the strength of the interactions between the particles.
In the plot on the right we show decay curves of the number of atoms in our trap as a function of time at different interaction strengths a. We fit these curves to extract the loss rate coefficient.
The extracted loss rate coefficient data shows many features that punctuate an overall $a^4$ scaling.
On the right hand side of the figure, (where a<0) an Efimov resonance is determined from an enhancement in the loss rate at a1-. On the left hand side (where a>0), we see two recombination minima, due to quantum interference, at $a_1^+$ and $a_2^+$ (separated by a factor of 16), along with an atom-dimer resonance associated with the second Efimov trimer at $a_2^*$. The solid black lines are fits to a universal theory, and the dashed black line shows the overall $a^4$ scaling. From theory, we expect the recombination minima to differ by a factor of 22.7; however, non-universal effects (see more below) may shift the resonance locations, resulting in deviations from theory. We also see new features ($a_{1,1}^T$) which may be associated with four-body physics.
The universality seen between three bodies is expected to extend to conditions when a fourth is added. We extract the four-body loss rate coefficient simultaneously with the three-body one when fitting the decay curves. The figure below shows our results, along with an extended Efimov energy diagram including the four-body tetramer energy levels [4].
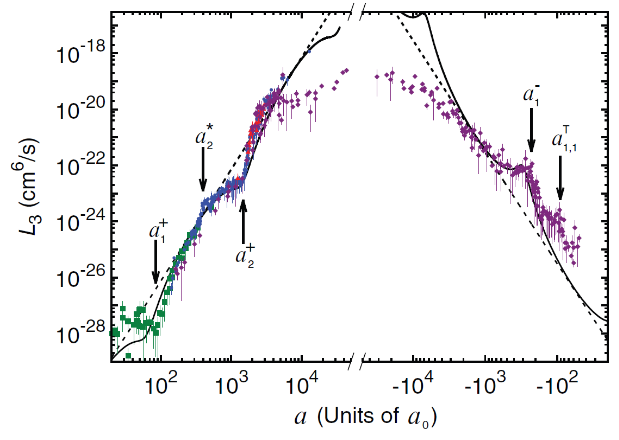
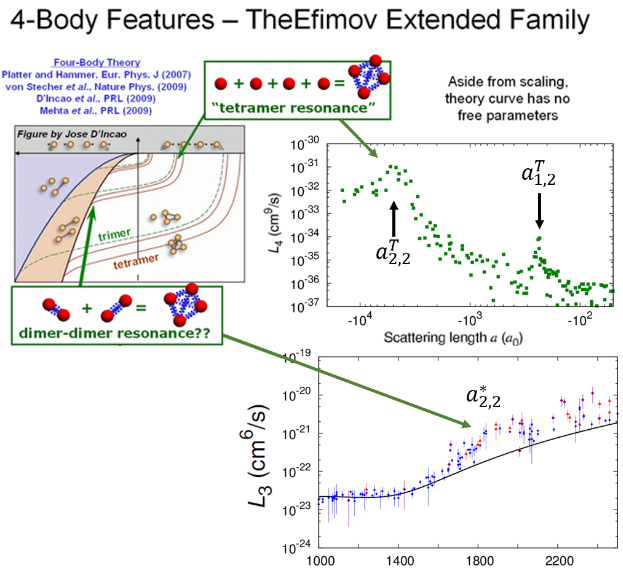
The locations of the observed features reflect on the universal nature of Efimov physics. Deviations from the predicted locations lend insight into the influence of the short-range physics (that’s the physics that was neglected in the universal theory) and temperature.
Temperature is a conveniently controllable parameter that allows us to explore deviations from universality, which become particularly relevant for negative scattering lengths, where the attractive interactions are not suitable for forming a condensate. Determination of the temperature dependence of resonance locations allow us to extrapolate to a zero-temperature value, and by comparing our results with predictions theorists can formulate a more complete theory of few-body physics.
Reference
[1] “Quantum Physics: A ménage à trois laid bare”, B. D. Esry and C. H. Greene, Nature 440, 289-290 (15 March 2006).
[2] “Extreme Tunability of Interactions in a 7Li Bose-Einstein Condensate”, S. E. Pollack, D. Dries, M. Junker, Y. P. Chen, T. A. Corcovilos, and R. G. Hulet, Physical Review Letters 102, 090402 (2009).
[3] “Observation of an Efimov spectrum in an atomic system”, M. Zaccanti, B. Deissler, C. D’Errico, M. Fattori, M. Jona-Lasinio, S. Muller, G. Roati, M. Inguscio, G. Modugno, Nature Physics 5, 586-591 (2009).
[4] “Rave Reviews for the Efimov Quartet”, JILA Research News (Summer 2009).
[5] “Finite range corrections near a Feshbach resonance and their role in the Efimov effect”, P. Dyke, S. E. Pollack, and R. G. Hulet. Physical Review A 88, 023625 (2013).
[6] “Universality in Three- and Four-Body Bound States of Ultracold Atoms”, S. E. Pollack, D. Dries, and R. G. Hulet, Science 326, 1683 (2009).